확률 모델(Probabilistic Models)
: 어떠한 상황을 가정하여 확률을 따지기 위한 것. 다음의 2가지로 이루어진다.
1. 표본 공간(Sample Space, Ω)
: 일어날 수 있는 모든 경우의 수가 전부 원소인 집합.
ex) a coin toss : Ω= {H, T}
ex) 2 coin toss : Ω = {HH, HT, TH, TT}
- 사건(Event) : 표본 공간의 부분 집합이다. 특정한 조건 하의 원소들이다.
ex) 2번의 동전 던지기에서 앞면이 한번이라도 나올 경우 A = {HH, HT, TH}
표본 공간(Sample Space)의 조건
- 원소들 끼리 서로 동시에 일어날 수 없어(mutually exclusive)야 한다. (unique outcome)
- 모든 결과(경우)가 포함되어야 한다. (Collectively Exhaustive)
ex) 2 coin tosses Ω = {HH, HT, TH} 는 틀렸다. TT라는 경우를 빼먹었기 때문이다.
데카르트 곱(Cartesian Product)
집합 A, B, C를 A x B x C 한다고 하자(데카르트 곱을 하는 것)
이는 곧 A 원소 중 하나, B 원소 중 하나, C 원소 중 하나를 뽑은 것이 하나의 원소고
그런 모든 경우의 수가 모인 표본 공간을 만든다는 것이다.
Ω = {x, y, z} x ∈ A, y ∈ B, z ∈ C
2. 확률 법칙(Probability Law, P())
: 사건을 매개인자로 가지는 함수이다.
- 0부터 1까지의 실수 값만을 가진다. P : A− > [0, 1], A ⊆ Ω
확률 법칙의 조건(Requirements for P)
모든 사건 A에 대하여, P(A)는 다음을 만족한다.
확률 공리(Probability Axioms)
|
공리 2번 적용 예)

!주의! : fair = equally likely = equal probability = 일어날 확률이 같다.
ex) P(Ω) = {1, 2, 3, 4, 5} each outcome is equal probabilty of 1/5
이산 확률 법칙(Discrete Probability Law)
Ω = {w1 , . . . , wn} 이 때, Ω는 유한의 혹은 셀 수 있는 집합이다.
event A = {w1 , . . . , wk} k ≤ n P(A) = P({w1})+. . . +P({wk})
-> 공리 2번이 그대로 적용되었음을 알 수 있다.
위의 법칙에서 P(wi) = 1 n , ∀i = 1, . . . , n 이라는 조건이 추가되면(uniform probability)
P(A) = k n (k = |A|) 가 성립한다. 원소 개수 만큼 확률이라는 뜻.
연속 확률 모델(Continuous Probability Model)
Example 1)
연속 확률 모델에서는 확률이 1이어도 안 일어날 수도, 확률이 0이어도 일어날 수도 있다.

그래서 실제로 존재하는 원소이지만, 확률이 0이거나
실제로 존재하는 원소를 제외했지만 확률이 1일 수가 있다.
(=> almost sure event = almost surely with probability 1)
ex) P(Ω) = P([0, 1]) = P([0, 1/2 ) ∪ ( 1/2 ) ∪ ( 1/2 , 1]) = P(A : [0, 1/2 ) ∪ ( 1/2 , 1])
P( 1/2 ) = 0 (그래서 뽑았을 때 절대로 안나온다? 현실에서? 그건 아니다)
Ω = sure event
A = almost sure event(almost surely with probability 1)
Example 2)
이산 확률과 마찬가지로, 공리 3가지를 모두 만족한다.
예시로 예시로 P(A) = length(A), ∀A ⊆ Ω = [0, 1]가 있다.
(만약 Ω = [0, 4]이면, 나누기 4를 해주면 된다. 그게 정규화)
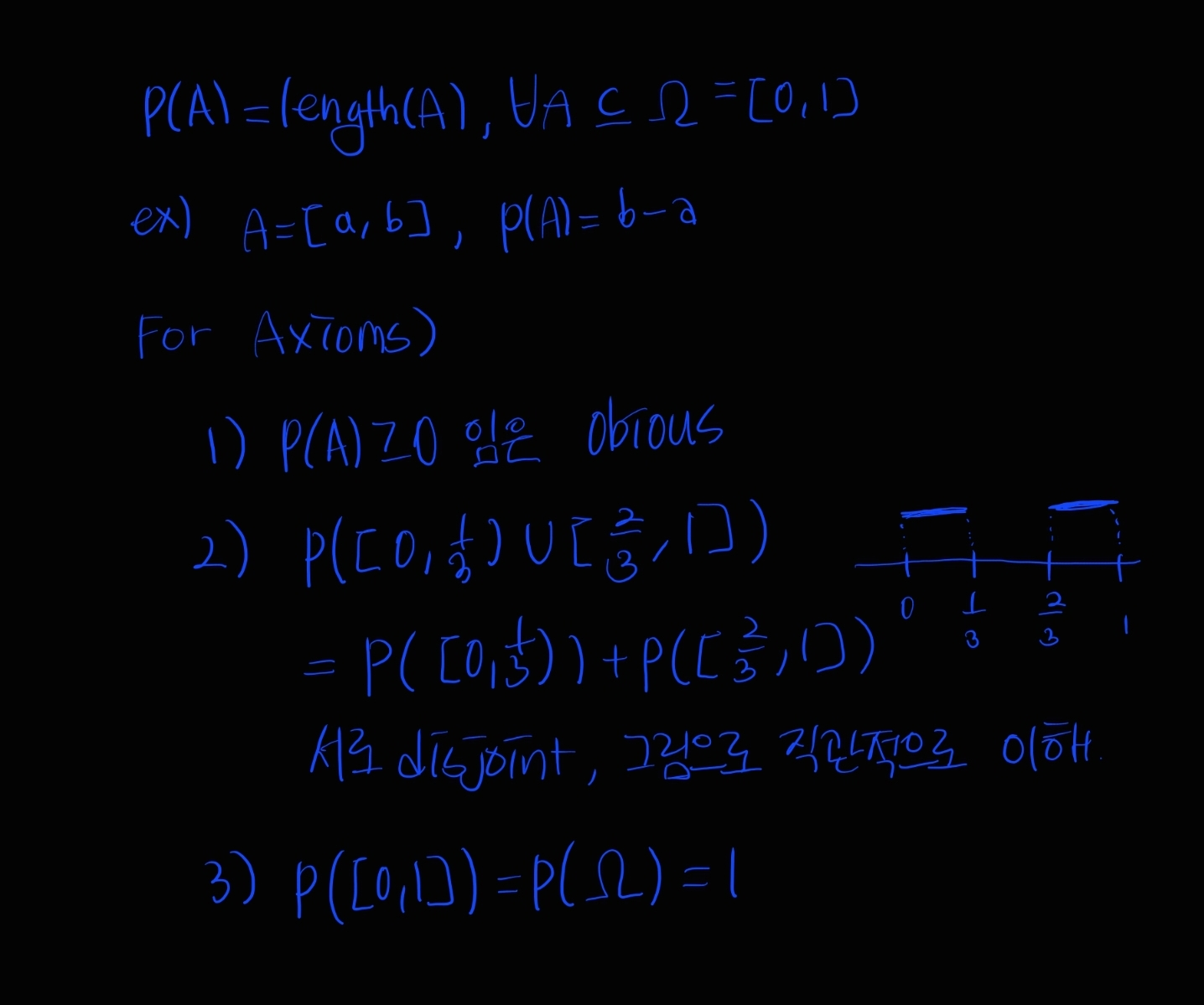
Example 3)
표본 공간이 예시 2번의 제곱이면 어떨까?
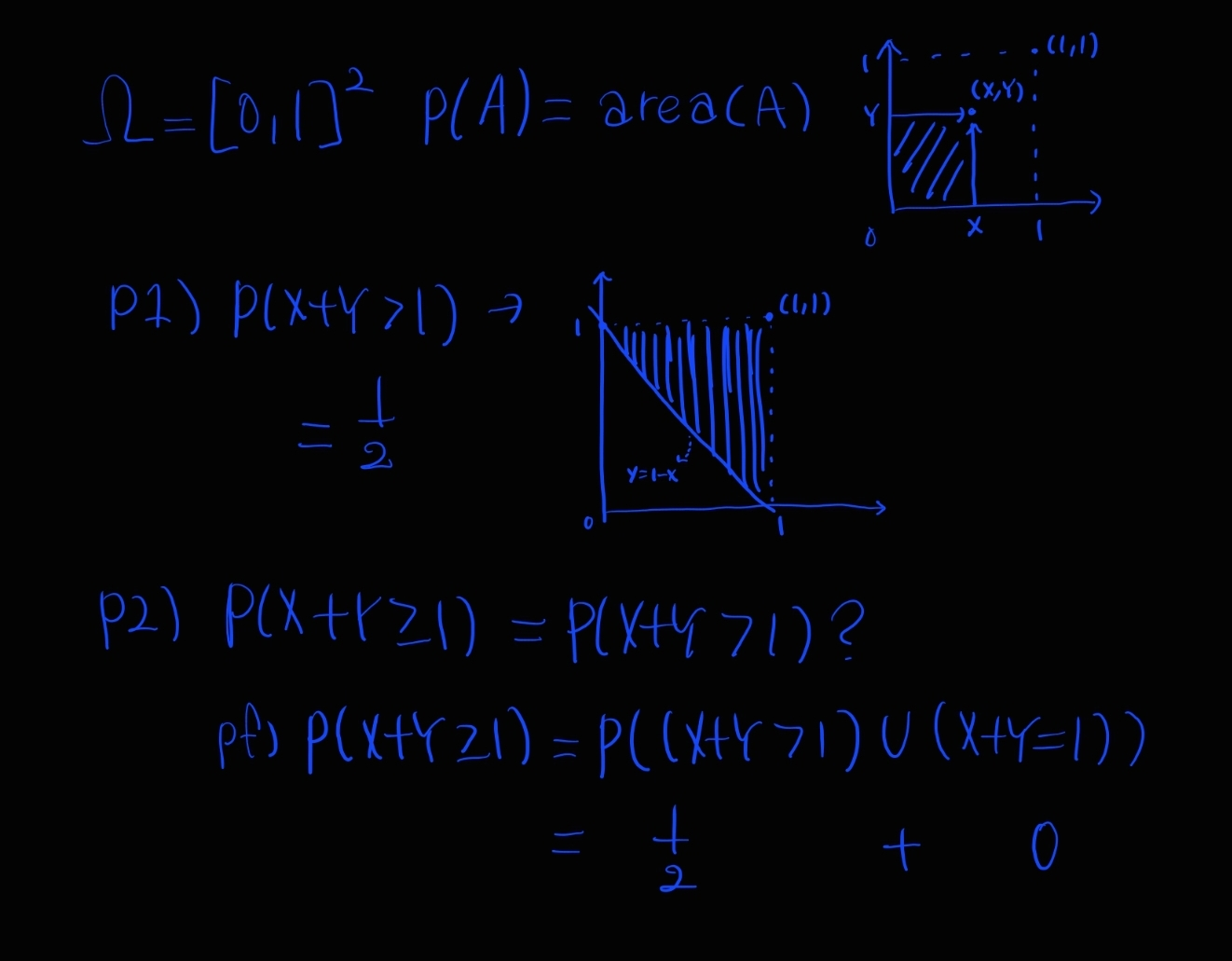
확률의 몇가지 속성들(Properties of Probability Laws)
- A가 B의 부분집합이면, P(A) ≤ P(B)
- P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
아래는 증명이다.
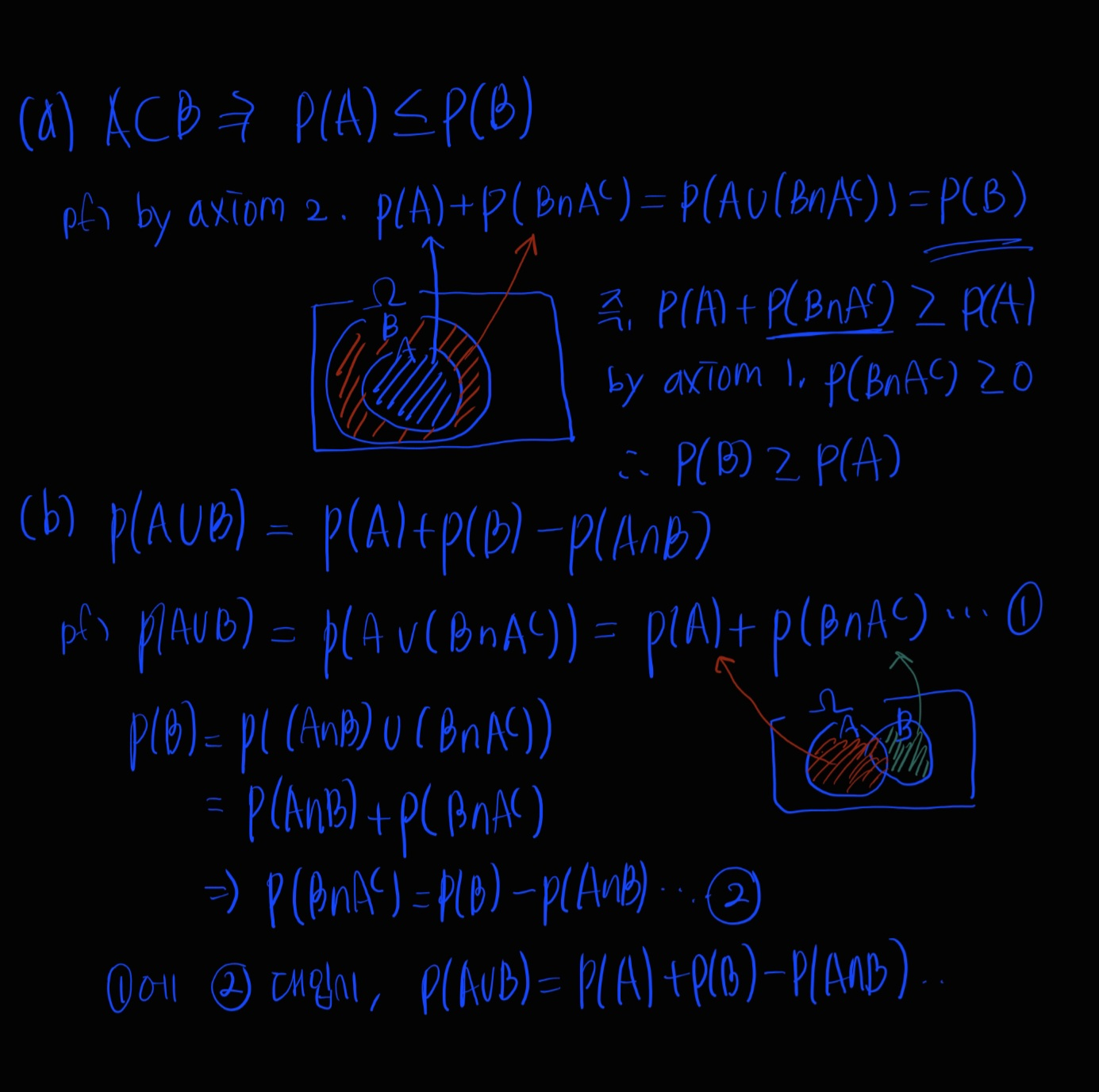
'Computer Science > 확률과 통계' 카테고리의 다른 글
| 확률 세기(Counting), 순열(Permutation)과 조합(Combination) (0) | 2024.07.06 |
|---|---|
| 독립(Independence)과 이항확률(Binomial Probabilities) (0) | 2024.07.06 |
| 전확률 공식, 베이즈 정리 (0) | 2024.07.04 |
| 조건부 확률(Conditional Probability) (1) | 2024.07.03 |
| 집합(Sets) (0) | 2024.07.03 |