확률 변수(Random Variables)
결과를 숫자로 대응시키는 것. 어떻게 보면 함수같은 느낌이다.
(질문을 통계학적으로 표현하는 것: number of heads = r(X) = {0, 1, 2})
random variable X:
$$X: \Omega ->R, X(w) \in R $$
간편하게 X=x라는 형태로 사용한다.
이산 확률 변수(Discrete Random Variables, DRV)
I. 이산(Discrete):
r(X)가 countable이면 이산(discrete)적인 것이다.
ex) sample space가 uncountable 이여도, r(X)가 countable인 경우:
| choosing a point p from [-1,1] -> $\Omega = [-1, 1]$ is uncountable X = {if p>0: 1 | if p=0: 0 | if p<0: -1} -> r(X) = {-1, 0, 1} is countable 결론은 countable하다. |
II. X는 X(w)=x 가 존재하면 있는 것이다.
ex) X is number of heads (in two tosses of a fair coin)
X(0) = {TT}, r(X(0)) = r({TT}) = $\frac{1}{4}$
X(3) = $\phi$, r(X(3)) = r($\phi$) = 0 (없는 것)
확률 질량 함수(Probaility Mass Functions, PMF)
X=x일 때(x가 정의역) 의 확률 값을 치역으로 하는 함수.
$$P_X(x) = P({X=x}) = P({w \in \Omega|X(w) = x})$$
ex) two independent tosses of a fair coin
X = number of Heads
$P_X(x)$ = {if x=0 or 2: $\frac{1}{4}$ | if x=1: $\frac{1}{2}$ | 나머지(otherwise, ow): 0}
X = 1(앞면이 1번 나온 event) 경우, P(X=1) = $P({w\in\Omega, X(w)=0})$= P({HT, TH}) = $\frac{1}{2}$
확률 질량 함수의 성질(Properties of PMF)
I. 확률 변수들(X=x)은 서로 서로소(disjoint)이고 표본 공간의 분할이다(partition of $\Omega$)
=> PMF를 전부 더하면 1이 된다.

II. X=x에서, 집합 S가 x의 가능한 값들이라고 하자. $\displaystyle P(X \in S) = \sum_{x\in S}^{}p_X(x)$ 이다.
=> 한마디로, $x_1, x_2, x_3..$의 확률의 합은 그 친구들 각각의 확률 더한것이다. (자연스러운)
!주의! : 모든 X=x의 확률 합이 반드시 1이어야 PMF인 것이다.
몇 가지의 이산 확률 변수 종류
이진 확률 변수(Binomial Random Variables)
동전 던지기 같은 binomial probability의 경우이다.
$p_X(k) = P(X=k) = nCkp^k(1-p)^{n-k}$ 로 표현된다.
모든 가능한 k값의 합은 normalization에 의해 1이다.
기하 확률 변수(Geometric RV)
앞면이 나올 때까지 동전 던지기를 하는 경우와 같다. (repeatedly and independently)
X = number of tosses until a head comes up
PMF : $p_X(k) = p(p-1)^{k-1}$ (head 나올 때까지 k-1번의 tail 나옴)
심화된 버젼이 HyperGeometric Distribution.
포아송 확률 변수(Poisson RV)

PMF of a Poisson RV with parameter $\lambda$

포아송 PMF 확률 합이 1이라는 것 증명(ft. 테일러 전개):
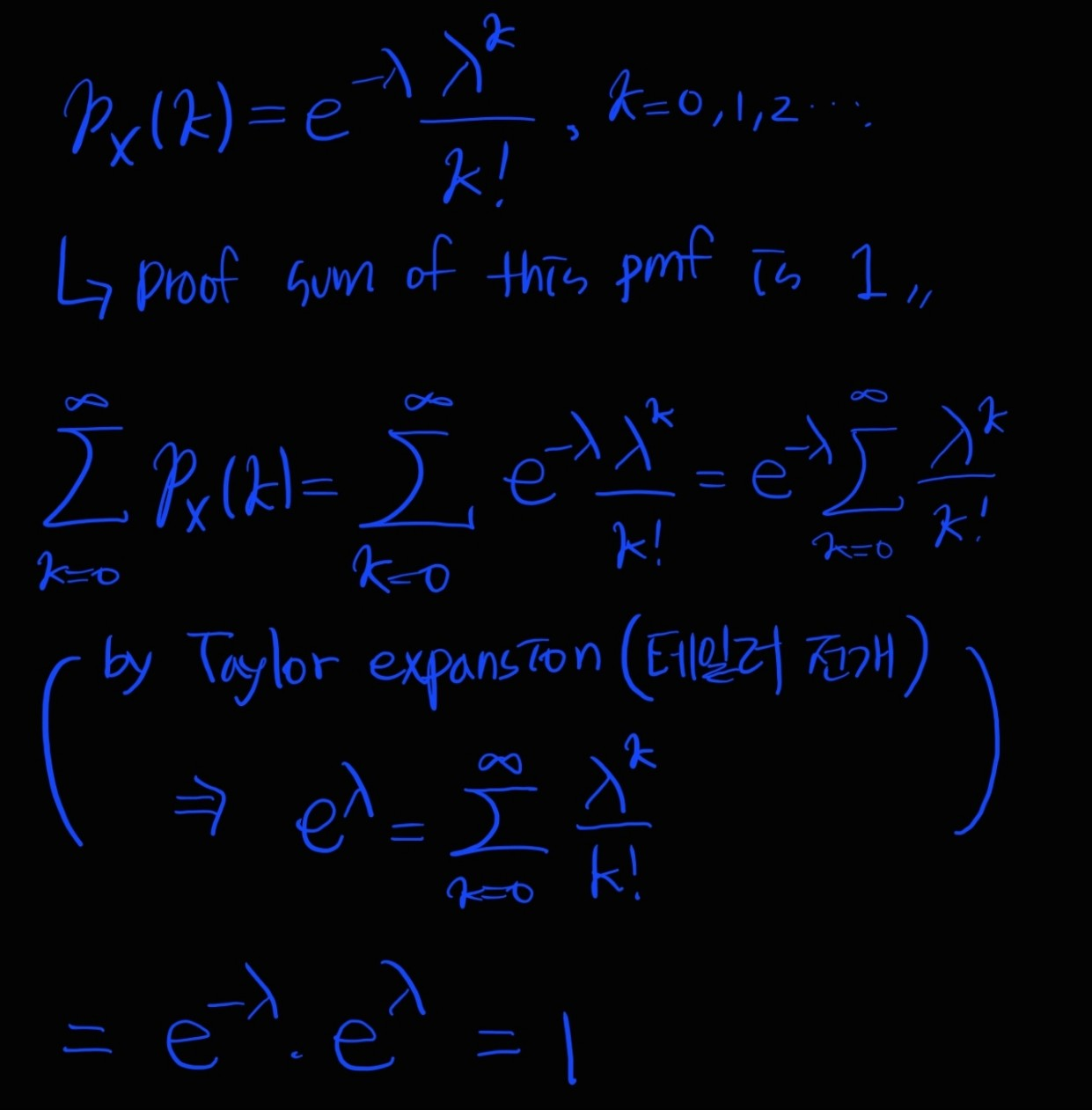
Binomial RV(이항 확률 변수)와 관련성
만약 이항 분포에서 n이 매우 크고, p가 상대적으로 매우 작다면.
이항 분포를 포아송 분포로 근사할 수 있다!
$$e^{\lambda}\frac{\lambda^k}{k!} = \frac{n!}{k!(n-k)!}p^k(1-p)^{n-k}\space\space if\space\space k << n$$
이때 $\lambda = np$이다.
'Computer Science > 확률과 통계' 카테고리의 다른 글
| 결합 확률 질량 함수(Joint PMF) (0) | 2024.07.10 |
|---|---|
| 평균과 분산(Mean and Variance) - DRV 관점에서 (0) | 2024.07.08 |
| 확률 세기(Counting), 순열(Permutation)과 조합(Combination) (0) | 2024.07.06 |
| 독립(Independence)과 이항확률(Binomial Probabilities) (0) | 2024.07.06 |
| 전확률 공식, 베이즈 정리 (0) | 2024.07.04 |