기댓값(Expectation=Mean=Expected Value)
기댓값은 PMF(확률질량함수)를 한마디(숫자)로 표현할 수 있다.
ex) 학생들 점수가 막 40점, 50점, 20점.. vs 학생들 평균(기댓값) 30점입니다.
$$E[X] = \sum_{x}^{} xp_X(x)$$
$\sum$ 확률 변수 x 확률 = 기댓값(평균)
- 기댓값의 여러 해석
Center of gravity of PMF : 확률 '질량' 함수의 가운데(평균) 이라는 뜻
Average in large number of repetitions of the experiment: 실행 횟수가 많은 실험의 예상되는평균 값
Example) two independent coin tosses

이산 확률 변수(DRV)에서 기댓값이 존재할 조건(언제나 그런건 아니다)
I. X가 유한해야 한다
II. $E[X] = \displaystyle\sum_{x}^{} xp_X(x)$의 값이 유한해야 한다
Example) $p_X(k) = \frac{1}{k(k+1)}, k \ge 1$의 E(x)

기댓값의 선형 성질(Linearity of Expectation)
a, b는 상수
- E[a] = a for constant a
- E[aX] = aE[X] (동차성)
- E[aX + b] = aE[X] + b (가산성 = 더하기는 그대로 나온다 ㅇㅇ)
(ex. E(X+X) = E(X) + E(X), E(E(X)) = E(X))
분산(Variance)
얼마나 퍼져있는가의 정도. (분산이 클수록 고르게 퍼졌다)

$X-E[X]$ = 평균으로부터 떨어진 거리(a measure of dispersion)
$E[(X-E[X])^2]$ = 평균으로부터 떨어진 거리의 제곱의 평균 = 분산(Variance)
이라고 생각하면 편하고, 공식은 아래와 같다.
$$V(X) = E[(X-E[X])^2] $$
표준 편차(Standard Deviation)
$$\sigma_X = \sqrt{V(X)} $$
표준 편차는 분산의 제곱근이다.
확률 변환(Expectaion of Functions of RVs; X를 함수로)
확률 변수 X=g(X)라는 함수로 대응시켜서 표현한다면 어떻게 되는가.
결국에는 (g(X)가 되는 X의 확률)xg(x) 의 합이다.

공식은 다음과 같다.
X는 DRV(이산확률변수)이고 X에 대한 함수 g(X)가 있다고 하자. 그렇다면,
$$E[g(X)] = \sum_{x}^{}g(x)p_X(x)$$
이 성립한다. (CRV(연속확률변수)의 경우는 $p_X(x)$를 $f_X(x)$로 하고 적분으로 바꾸어준다)
증명:
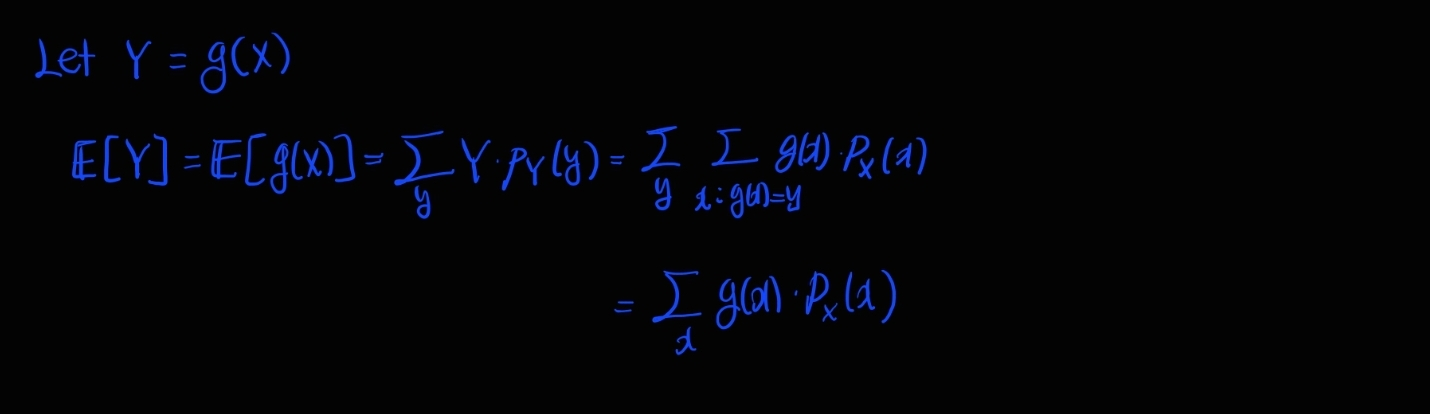
그래서 분산을 다음과 같이 표기할 수도 있다.
$\displaystyle V(X) = \sum_{x}{}(x-E[X])^2p_X(x) = E[(x-E[x])^2]$
예시와 비교하자면 $Y = (x-E[x])^2$ 인 셈이다.
분산의 성질
I. 확률 변수의 계수는 분산에서 제곱이고, 상수는 영향을 주지 못한다.
$$V(aX + b) = a^2V(X)$$

II. 분산은 (확률 변수 제곱의 평균 - 평균의 제곱)과 같다.
$$V(X) = E[X^2] - (E[X])^2$$

'Computer Science > 확률과 통계' 카테고리의 다른 글
| 조건부 이산 확률 변수, 확률 질량 함수, 기댓값 (0) | 2024.07.16 |
|---|---|
| 결합 확률 질량 함수(Joint PMF) (0) | 2024.07.10 |
| 이산 확률 변수(Discrete Random Variable, DRV) (0) | 2024.07.08 |
| 확률 세기(Counting), 순열(Permutation)과 조합(Combination) (0) | 2024.07.06 |
| 독립(Independence)과 이항확률(Binomial Probabilities) (0) | 2024.07.06 |