여러 확률 변수의 결합 확률 질량 함수(Joint PMFs of Multiple RVs)
DRV인 두 확률 변수 X, Y가 있다고 하자.
두 PMF를 합치면(Joint PMF)
$$p_{X,Y}(x, y) = P(X=x, Y=y) = P({X=x}\cap{Y=y})$$
Example)

P((X, Y) $\in$ A), P((x, y) : $0 \le x \le 1, 1 \le y \le 2$) 의 값은,

주변 확률 질량 함수(Marginal PMFs)
Joint PMF는 각각의 PMF를 다 포함했기에, Joint PMF를 알면 결국 각각의 PMF를 알 수 있다.
증명에는 각각의 DRV들이 결국 표본 공간의 분할임을 이용, 전확률정리를 사용한다.

marginal 개념은 아래 개념들에서 증명하는데 계속 쓰인다.
다중 확률 변수의 변환(Functions of Multiple RVs)
확률 변환에서 확률 변수 갯수만 늘어난 것이다.

선형 성질에 따라 다음이 성립한다.
g(x, y) = ax + by + c => E[g(X, Y)] = aE[X] + bE[Y] + c
증명은 다음과 같고, marginal 개념이 들어가 있다.
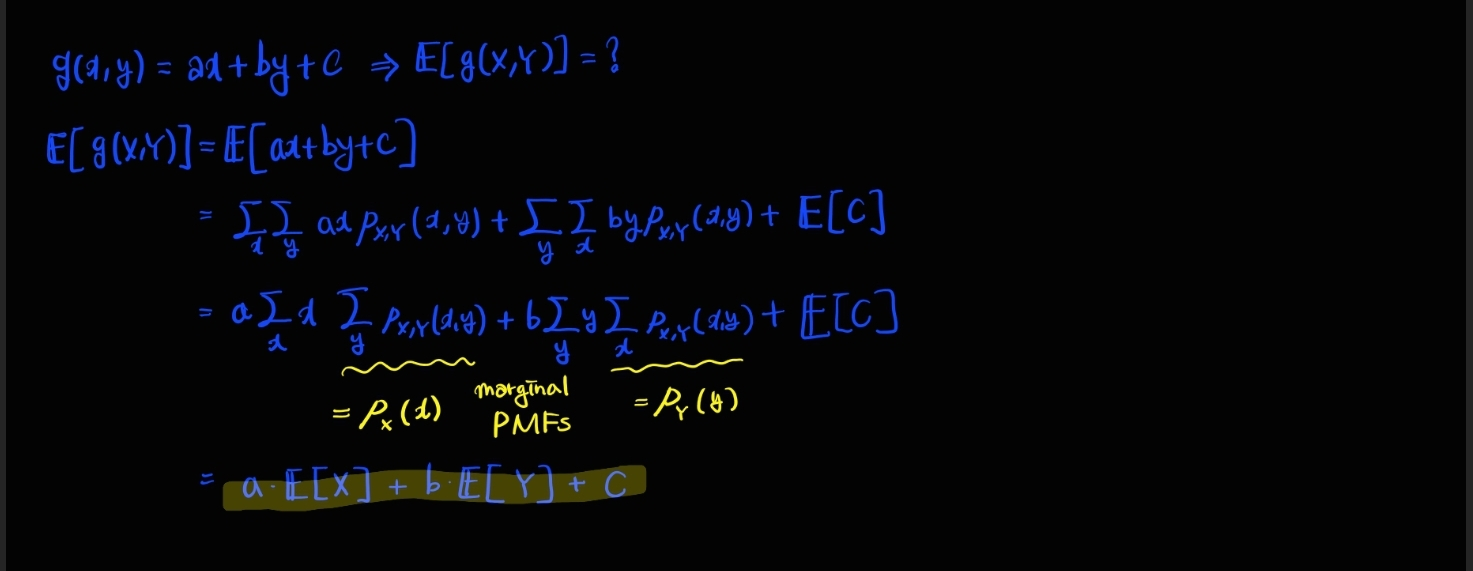
여러 확률 변수의 결합 확률 질량 함수(Joint PMFs of Multiple RVs)
DRV인 세 확률 변수 X, Y, Z가 있다고 하자.
Joint PMF: $$p_{X, Y, Z}(x, y, z) = P(X=x, Y=y, Z=z) $$
Marginal PMFs:$$P_{X, Y}(x, y) = \sum_{z}{}P_{X, Y, Z}(x, y, z) $$
$$P_X(x) = \sum_{y}{}\sum_{z}{}p_{X, Y, Z}(x, y, z) $$
Expectation:$$E[g(X, Y, Z)] = \sum_{x}{}\sum_{y}{}\sum_{z}{}p_{X, Y, Z}(x, y, z) $$
if g = aX + bY + cZ + d: $$E[g(X, Y, Z)] = aE[X]+bE[Y]+cE[Z]+d $$
일반화 하면(In general):$$E[a_1X_1 + ... + a_nX_n] = a_1E[X_1] +...+a_nE[X_n] $$
Example)
베르누이 시행의 평균을 위 일반화를 이용하여 쉽게 구할 수 있다.
베르누이 시행 $X_i = (P(1) = p$ or $P(0) = 1-p)$
$$E[\sum^n_{i=1}X_i] = \sum^n_{i=1}E[X_i] = np = p+..+p +0(1-p)+..+0(1-p)$$
'Computer Science > 확률과 통계' 카테고리의 다른 글
| 조건부 이산 확률 변수, 확률 질량 함수, 기댓값 (0) | 2024.07.16 |
|---|---|
| 평균과 분산(Mean and Variance) - DRV 관점에서 (0) | 2024.07.08 |
| 이산 확률 변수(Discrete Random Variable, DRV) (0) | 2024.07.08 |
| 확률 세기(Counting), 순열(Permutation)과 조합(Combination) (0) | 2024.07.06 |
| 독립(Independence)과 이항확률(Binomial Probabilities) (0) | 2024.07.06 |